Modelling and Solving
with Choco-solver
Charles Prud'homme, Sept. 2025IMT Atlantique, LS2N, TASC
< press [N] / [P] to go the next / previous slide >
We will see
- A short presentation of Choco-solver
- The key elements of modelling and solving
- Some ways of extending the library
- Playing with some problems
We will not see
- What is Constraint Programming
- How a constraint solver works, see this presentation instead
- High-level modelling languages like XCSP$^3$ / PyCSP3, MiniZinc, CPMpy, …
Choco-solver
Features
- Parsers for XCSP$^3$, MiniZinc and DIMACS CNF files
- Included in PyCSP3 (
-solver=choco) - As tier 3 solver in CPMpy (since 0.9.17)
- About 3 releases per year
- 4.10.16 is the current version
- $\approx5,860$ downloads per month, according to MCR
- 5 types of variable available
- $> 200$ propagators
- State-of-the-art search strategies
- Almost LCG-ready
Visit the website for more documentation, tutorials, javadoc , etc
Getting Started
- JRE 11+ installed (Oracle or OpenJDK)
- Easier with:
- an IDE: IntelliJ IDEA, Eclipse IDE, Apache NetBeans or VSCode
- a build automation tool: Apache Maven 3+ or Gradle 6+
A first example
int n = 8;
Model model = new Model(n + "-queens problem");
IntVar[] vs = model.intVarArray("Q", n, 1, n);
model.allDifferent(vs).post();
for(int i = 0; i < n-1; i++){
for(int j = i + 1; j < n; j++){
model.arithm(vs[i], "!=", vs[j], "-", j - i).post();
model.arithm(vs[i], "!=", vs[j], "+", j - i).post();
}
}
Solution solution = model.getSolver().findSolution();
if(solution != null){
System.out.println(solution.toString());
}
Modelling
Creation of a Model instance
Model is the central object
in the Choco-solver library
- Creating a model is the first essential step in declaring and solving a problem.
- Variables are declared via the model
- Constraints too
In fact, almost anything can be done via a Model instance$^1$.
$1$: So you don’t have to know all the objects in advance.
Several builders
Model m = new Model(); // 1
Model m = new Model(String name); // 2
Model m = new Model(settings settings); // 3
Model m = new Model(String name, Settings settings); // 4
Prefer choices 1 and 2 to start with.
package apetizer;
public class Example{
public static void main(String[] args){
}
}
package apetizer;
import org.chocosolver.solver.Model;
public class Example{
public static void main(String[] args){
Model myModel = new Model("My first model");
}
}
Variables and domains
A variable
- is a symbolic representation of an unknown quantity/decision,
- comes with potential values that the solver can assign to it, a.k.a. its domain,
- to be determined/assigned during the problem-solving process.
In a scheduling problem
- Variables : the start time of various tasks
- Domains : the set of possible start time slots

In a packing problem
- Variables : the assignment of items to bins
- Domains : the set of possible bins

In a routing problem
- Variables : the nodes visited on a tour
- Domains : the potential successors of each node

Different types of variables are available:
IntVarhas its values in $\mathbb{Z}^1$IntViews relies on anIntVar- like
IntAffineView
- like
BoolVar(andBoolView) has its values in {$0,1$}- sub-type of
IntVar
- sub-type of
Taskto manage with task/interval: $s+d = e$SetVarandSetView(Un)DirectedGraphVarandGraphView- and also
RealVar
Ways to declare integer variables
Model m = new Model();
IntVar x = m.intVar("x", 0, 4);
IntVar y = m.intVar("y", new int[]{1,3,5});
IntVar[] vs = m.intVarArray("v", 4, 1, 3);
IntVar[][] ws = m.intVarMatrix("w", 2, 2, 1, 2);
Ways to declare Boolean variables
Model m = new Model();
BoolVar b = m.boolVar("b");
BoolVar[] bs = m.boolVarArray("bs", 10);
BoolVar[][] bss = m.boolVarMatrix("bss", 4, 3);
Similar APIs for other types of variables.
Some views declaration
Model m = new Model();
IntVar x = m.intVar("x", 0, 5);
IntVar v = m.intView(2, x, -3); // v = 2.x - 3
BoolVar b = m.isEq(x, 2); // b = (x == 2)
BoolVar n = b.not(); // n = !b
And also abs(x), mu(x, 2), neg(x), isLeq(x, 3), …
Reading a variable
Model m = new Model();
IntVar x = m.intVar("x", 0, 4);
System.out.printf("Variable : %s = [%d, %d]\n",
x.getName(), x.getLB(), x.getUB());
System.out.printf("%s is %s instantiated\n",
x.getName(), x.isInstantiated() ? "" : "not");
outputs
Variable : x = [0, 4]
x is not instantiated
If instantiated, a variable can return its assignment value with x.getValue().
ABCDE x 4 = EDCBA
If ABCDE times 4 equals EDCBA, and each letter is a different digit from 0 to 9,
what is the value of each letter?
A Model
-
Variables:
- $\forall i \in \{a,b,c,d,e\}, l_i \in [\![ 0,9]\!]$
-
Constraints :
- $\forall i\neq j \in \{a,b,c,d,e\}, l_i \neq l_j$
- $39999l_a + 3990l_b + 300l_c - 960l_d - 9996l_e = 0$
Choco-solver code
// Create a model
Model model = new Model("ABCDE x 4 = EDCBA");
// Declare the variables with their initial domain
IntVar A = model.intVar("A", 0, 9);
IntVar B = model.intVar("B", 0, 9);
IntVar C = model.intVar("C", 0, 9);
IntVar D = model.intVar("D", 0, 9);
IntVar E = model.intVar("E", 0, 9);
// Constraint 1:
// "each letter is a different digit from 0 to 9"
// the second part of the constraint is defined
// by the domain of each variable
model.allDifferent(A, B, C, D, E).post();
// Constraint 2:
// "org.step1.ABCDE times 4 equals EDCBA"
// 40000 A + 4000 B + 400 C + 40 D + 4 E = 10000 E + 1000 D + 100 C + 10 B + A
// <=> 39999 A + 3990 B + 300 C + -960 D - 9996 E = 0
model.scalar(
new IntVar[]{A, B, C, D, E},
new int[]{39_999, 3_990, 300, -960, -9_996},
"=", 0).post();
// Find a solution and print it
if (model.getSolver().solve()) {
int[] sol = new int[]{A.getValue(), B.getValue(), C.getValue(), D.getValue(), E.getValue()};
System.out.printf(" %d%d%d%d%d\nx 4\n------\n %d%d%d%d%d\n",
sol[0], sol[1], sol[2], sol[3], sol[4],
sol[4], sol[3], sol[2], sol[1], sol[0]);
}else{
System.out.println("No solution found");
}
Output
21978
x 4
------
87912
Can you guess his year of birth?
Someone comes up to you and says:
On my birthday in 2025, my age will be equal to the sum of the digits of my birth year. I am less than 100 years old. What could my birth year be?
Can you model this as a CP problem?
A Model
- Parameters
- $input$: the current year
- Variables
- $\forall i \in \{th,hu,te,on\}, x_i \in [\![0,9]\!]$
- $age \in [\![0,99]\!]$
- Constraints
- $x_{th} + x_{hu} + x_{te} + x_{on} = {age}$
- $1000x_{th} + 100x_{hu} + 10x_{te} + x_{on} + age = input$
Hints
model.sum(IntVar[], String, int)
model.scalar(IntVar[], int[], String, int)
A Choco-solver code
Model model = new Model("Age equals sum of birth year digits");
IntVar th = model.intVar("th", 0, 9);
IntVar hu = model.intVar("hu", 0, 9);
IntVar te = model.intVar("te", 0, 9);
IntVar on = model.intVar("on", 0, 9);
IntVar age = model.intVar("age", 0, 99);
model.sum(new IntVar[]{th, hu, te, on}, "=", age).post();
model.scalar(
new IntVar[]{th, hu, te, on, age},
new int[]{1_000, 100, 10, 1, 1},
"=", 2025).post();
while (model.getSolver().solve()) {
int[] sol = new int[]{th.getValue(), hu.getValue(), te.getValue(), on.getValue()};
System.out.printf("I was born in %d%d%d%d, I am %d years old\n", sol[0], sol[1], sol[2], sol[3], age.getValue());
}
if(model.getSolver().getSolutionCount() == 0) {
System.out.println("No solution found");
}
Output
I was born in 1998, I am 27 years old
I was born in 2016, I am 9 years old
Constraints
(and propagators)
A constraint
- represents a problem's requirements or limitations,
- defines a relationships among variables,
- expresses conditions that must be satisfied by the values assigned to the variables,
- is equipped with a filtering algorithm.
For example: $X < Y$
The goal of constraint programming is to find a combination of variable assignments that simultaneously satisfies all the specified constraints.
Basic constraints
| Constraint | Syntax | Comment |
|---|---|---|
| $x + y = z$ | m.arithm(x,"+",y,"=",z) |
Up to 3 variables |
| $\sum_i C_i\cdot X_i = 11$ | m.scalar(X,C,"=",11) |
See also m.sum(x,op,c) |
| $x\times y = z$ | m.times(x,y,z) |
Alt. Euclidean division |
| $y = |x|$ | m.absolute(y,x) |
Or view: y = m.abs(x) |
| $ |x-y | > 3$ | m.distance(x,y,">", 3) |
|
| $z = \max(x,y)$ | m.max(z,x,y) |
Alt. $\min$ |
| $\bigvee_i B_i$ | m.or(B) |
Alt. m.and(B) |
Adding a constraint to the model
Once a constraint has been created, it must be activated or reified
| Action | Syntax |
|---|---|
| Activate $c$ | c.post(); |
| $c \iff b$ | c.reifyWith(b);BoolVar b = c.reify(); |
| $c \implies b$ | c.implies(b); |
| $b \implies c$ | c.impliedBy(b); |
What if you want to express such a a non-linear constraint 🔋 ?

In extension
This can be achieved with a Table constraint
Model m = new Model();
IntVar c = m.intVar("SoC", 0, 100);
IntVar v = m.intVar("cV", 1140, 1280);
Tuples tuples = new Tuples();
tuples.add(100, 1273);
tuples.add(90, 1240);
tuples.add(80, 1235);
//...
tuples.add(20, 1195);
tuples.add(10, 1151);
m.table(c, v, tuples).post();
Types of Table constraints
Allowed tuples
Model m = new Model();
IntVar[] xs = m.intVarArray("x", 3, 1, 3);
// all equal
Tuples tuples = new Tuples();
tuples.add(1, 1, 1);
tuples.add(2, 2, 2);
tuples.add(3, 3, 3);
m.table(xs, tuples).post();
Forbidden tuples
Model m = new Model();
IntVar[] xs = m.intVarArray("x", 3, 1, 3);
// *not* all equal
Tuples tuples = new Tuples(false);
tuples.add(1, 1, 1);
tuples.add(2, 2, 2);
tuples.add(3, 3, 3);
m.table(xs, tuples).post();
Universal value
Like '*' symbol in regular expression.
Model model = new Model();
IntVar[] xs = m.intVarArray("x", 3, 0, 3);
Tuples ts = new Tuples();
int star = 99;
ts.setUniversalValue(star);
ts.add(3, star, 1);
ts.add(1, 2, 3);
ts.add(2, 3, 2);
model.table(xs, ts).post();
Hybrid tuples
Model model = new Model();
IntVar[] xs = m.intVarArray("x", 3, 1, 3);
HybridTuples tuples = new HybridTuples();
tuples.add(ne(1), any(), eq(3));
tuples.add(eq(3), le(2), ne(1));
tuples.add(lt(3), eq(2), ne(b));
tuples.add(gt(2), ge(2), any());
model.table(xs, tuples).post();
It is also possible to express a constraint from a variable
Expressions
| Family | Syntax |
|---|---|
| Arithmetic | x.neg() x.abs() x.sqr()x.add(i, …) x.sub(i, …) x.div(i) x.mod(i) x.pow(i) x.dist(i) x.max(i, …) x.min(i, …) |
| Relational | x.eq(i) x.ne(i) x.in(i, …) x.nin(i, …)x.lt(i) x.le(i) x.gt(i) x.ge(i) |
| Logical | x.not() x.imp(r) x.iff(r) x.ift(r1, r2) x.and(r, …) x.or(r, …) x.xor(r, …) |
$i$ is either an
int, a IntVar or an arithmetical expression,
$r$ is a relational expression.
Example
$(x = y + 1) \lor (x+2 \leq 6)$
IntVar x = //...
IntVar y = //...
x.eq(y.add(1)).or(x.add(2).le(6)).post();
Adding an expression to the model
Here again, there are different ways to work with an expression $e$, depending on its type:| Syntax | Ar. | Re. | Lo. |
|---|---|---|---|
e.post(); |
❌ | ✅ | ✅ |
c = e.decompose(); c = e.extension(); |
❌ ❌ |
✅ ✅ |
✅ ✅ |
x = e.intVar();b = e.boolVar(); |
✅ ❌ |
❌ ✅ |
❌ ✅ |
Sujiko
The puzzle takes place on a 3x3 grid with four circled number clues at the centre of each quadrant which indicate the sum of the four numbers in that quadrant.
The numbers 1-9 must be placed in the grid, in accordance with the circled clues, to complete the puzzle.
Empty grid
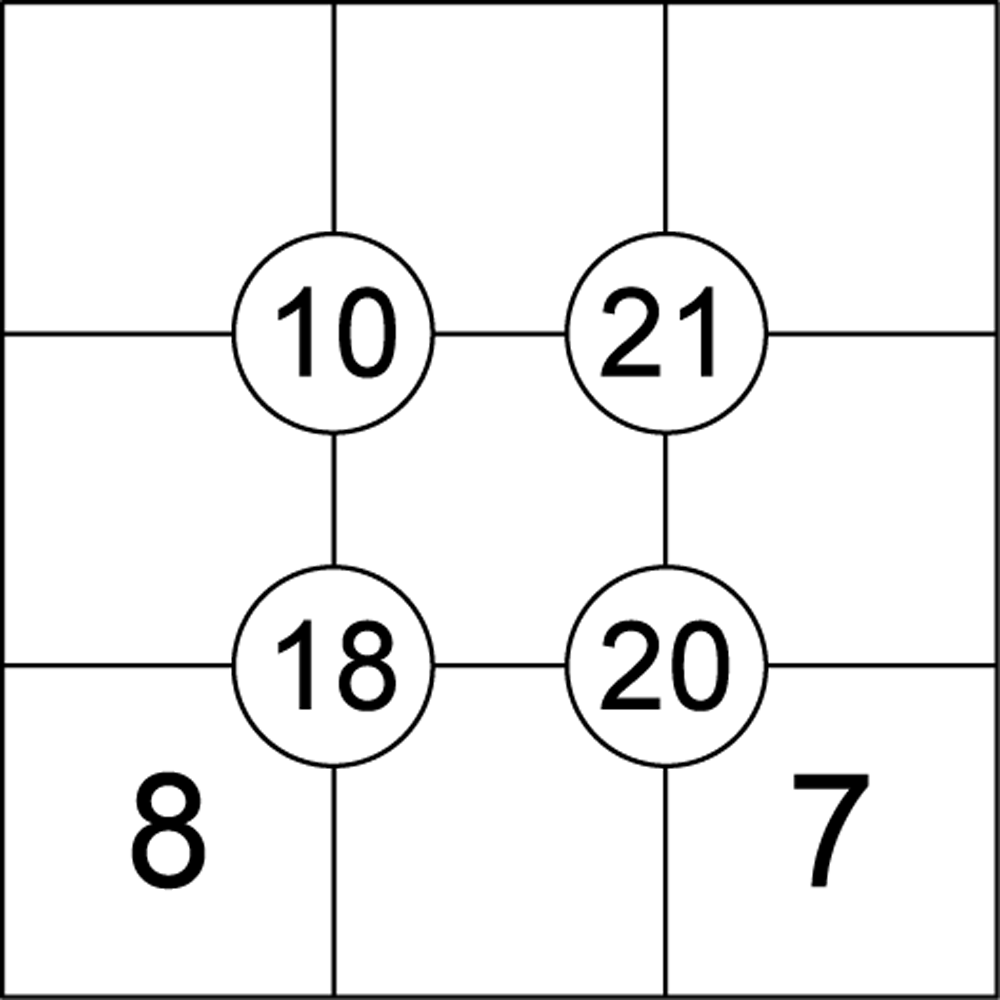
A Model
- Parameters
- $S_0, S_1, S_2, S_3$: the four circled number clues
- $f_{i,j}$: some fixed cells
- Variables
- $\forall i,j \in [\![0,2]\!]^2, x_{i,j} \in [\![1,9]\!]$
- Constraints
- $\forall i, i’, j, j’ \in [\![0,2]\!]^4, (i,j)\neq(i’,j’), x_{i,j} \neq x_{i’,j’}$
- $\forall i \in [\![0,3]\!], k = \frac{i}{2}, \ell = i \mod 2,$ $x_{k,\ell} + x_{k + 1,\ell} + x_{k,\ell + 1} + x_{k + 1,\ell +1} = S_i$
- +clues
Hints
model.allDifferent(IntVar[])
model.sum(IntVar[], String, int)
model.arithm(IntVar, String, int)
int[] circles = new int[]{10, 21, 18, 20};
int[] clues = new int[]{0, 0, 0, 0, 0, 0, 8, 0, 7};
private IntVar[] quadrant(IntVar[][] grid, int i) {
int x = i / 2;
int y = i % 2;
return new IntVar[]{grid[x][y], grid[x + 1][y], grid[x][y + 1], grid[x + 1][y + 1]};
}
A Choco-solver code
Model model = new Model("Sujiko");
IntVar[][] grid = model.intVarMatrix("x", 3, 3, 1, 9);
// Constraint: "The numbers 1-9 must be placed in the grid"
// implies that all values must be different
model.allDifferent(ArrayUtils.flatten(grid)).post();
// Constraint: "each quadrant which indicate the sum of the four numbers in that quadrant"
for (int i = 0; i < 4; i++) {
IntVar[] cells = quadrant(grid, i);
model.sum(cells, "=", circles[i]).post();
}
// Constraint: "the clues"
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
if (clues[i * 3 + j] != 0) {
model.arithm(grid[i][j], "=", clues[i * 3 + j]).post();
}
}
}
while (model.getSolver().solve()) {
System.out.println("Solution:");
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
System.out.print(grid[i][j].getValue() + " ");
}
System.out.println();
}
}
if (model.getSolver().getSolutionCount() == 0) {
System.out.println("No solution found");
}
Output
Solution:
1 4 9
3 2 6
8 5 7
Global Constraints
Definition(s)
an expressive and concise condition involving a non-fixed number of variables
allDifferent($x_1,x_2,\dots$)
Definition(s)
a constraint C is often called “global” when “processing” as a whole gives better results than “processing” any conjunction of constraints that is “semantically equivalent” to C
allDifferent($x_1,x_2,x_3$) $\iff (x_1\neq x_2) \land (x_2\neq x_3) \land (x_3\neq x_1)$
Example of constraints
cumulative(starts, durations, heights, capacity)

Example of constraints
binpacking(bins, weigths, capacity)

Example of constraints
circuit(successors)

Some cardinality constraints
| Syntax | Definition |
|---|---|
m.allDifferent(X) |
$x_i\neq x_j, \forall i< j$ |
m.among(n, X, v) |
$|x_i : x_i \cap v\neq \emptyset | = n$ |
m.count(y, X, n) |
$ | \{ x_i : x_i = y \} | = n$ |
m.nValues(X, n) |
$|x_i| = n$ |
Notations
- Arrays: $X=\langle x_0, x_1,\ldots\rangle$
- Index: $ 0 \leq i < |X|$
Some connection constraints
| Syntax | Definition |
|---|---|
m.element(v, X, i, o) |
$\exists i : v = x_{i - o}$ |
m.argmax(i, o, X) |
$i \in \{j - o : x_j = \max\{x_k\}\}$ |
m.argmin(i, o, X) |
$i \in \{j - o : x_j = \max\{x_k\}\}$ |
m.max(m, X) |
$m = \max\{x_i\}$ |
m.min(m, X) |
$m = \min\{x_i\}$ |
m.inverseChanneling(X, Y) |
$ \forall i: x_i = j \iff y_j = i \quad (|X| = |Y|)$ |
Notations
- Arrays: $X=\langle x_0, x_1,\ldots\rangle$
- Index: $ 0 \leq i < |X|$
Some Packing and Scheduling constraints
| Syntax | Definition |
|---|---|
m.binPacking(X, S, L, o) |
$ \forall b \in \{x_i\},\sum_{i : x_i = b} S_i \leq L_b$ |
m.cumulative(A, H, c) |
$ \forall t \in \mathcal{N},\sum\{h_i : a^s_i \leq t < a^e_i\} \leq c$ |
m.diffN(X, Y, W, H, true) |
$\forall i<j, x_{i} + w_{i} \leq x_{j} \lor x_{j} + h_{j} ≤ x_{i}$ $\quad\quad\quad \lor y_{i} + h_{i} \leq y_{j} \lor y_{j} + w_{j} ≤ y_{i}$ |
m.knapsack(O, W, E, w, e) |
$\sum_{i} w_i \times O_i = w \land \sum_{i} e_i \times O_i = e$ |
Notations
- Arrays: $X=\langle x_0, x_1,\ldots\rangle$
- Index: $ 0 \leq i < |X|$
- Task (or activity): $a^s + a^d = a^e$
Some Graph-based constraints
| Syntax | Definition |
|---|---|
m.circuit(X) |
$\{(i, x_i) : i \neq x_i\}$ forms a circuit of size $> 1$ |
m.path(X, s, e) |
$\{(i, x_i) : i \neq x_i\}$ forms a path from $s$ to $e$ |
m.tree(X, n) |
$\{(i, x_i) : i \neq x_i\}$ is partitioned into $n$ anti-arborescences |
Notations
- Arrays: $X=\langle x_0, x_1,\ldots\rangle$
- Index: $ 0 \leq i < |X|$
- A pair $(i, x_i)$ represents an arc in a graph induced by $X$
Magic Sequence
A magic series of length $n$ is a sequence of integers $[x_0, …, x_{n-1}]$ between $0$ and $n-1$, such that for all $i \in \{0 , …, n-1\}$, the number $i$ occurs exactly $x_i$ times in the sequence.
For instance, $[1,2,1,0]$ is a magic series of length $4$ :
- value 0 occurs once
- value 1 occurs twice
- value 2 occurs once
- value 3 does not occur
Write a CP model in java using the Choco solver to find magic series for any given n.
Solving
CSP
The solving process is managed by a unique Solver instance attached to a model.
Model model = new Model();
// ... problem description ...
Solver solver = model.getSolver();
if(solver.solve()){
// here you can read the variables' value
System.out.printf("%s is fixed to %d\n",
x.getName(), x.getValue());
}
A call to solver.solve() returns true if a solution exists, false otherwise.
CSP
The solving process is managed by a unique Solver instance attached to a model.
Model model = new Model();
// ... problem description ...
Solver solver = model.getSolver();
if(solver.solve()){
// here you can read the variables' value
System.out.printf("%s is fixed to %d\n",
x.getName(), x.getValue());
}
Since the solver stops on a solution,
all the variables are fixed and their value can be read.
CSP
The solving process is managed by a unique Solver instance attached to a model.
Model model = new Model();
// ... problem description ...
Solver solver = model.getSolver();
while(solver.solve()){
// here you can read the variables' value
System.out.printf("%s is fixed to %d\n",
x.getName(), x.getValue());
}
Enumerating solutions can be done in a while-loop.
Solution
We can capture the current state of variables in a Solution.
List<Solution> solutions = new ArrayList<>();
while(solver.solve()){
solutions.add(new Solution(model).record());
}
Solution
This can also be achieved in one line of code
Solution solution = solver.findSolution();
List<Solution> solutions = solver.findAllSolutions();
COP
An IntVar to maximize/minimize .
Solution bSol = solver.findOptimalSolution(obj, maximize);
List<Solution> bSols = solver.findAllOptimalSolutions(obj, max);
Solving is reducing
Backtracking algorithm
- recursive traversal of the search tree
- make/cancel decisions
- backtrack on failure
- incremental construction of a solution
Branch and Propagate
⚠️ 2-way branching
Making decisions
Can't we just leave it to the solver?
Bring business knowledge
Help moving towards a solution
but Yes, we can
Making decisions
- choose a free variable (how?)
- select an operator (very often $=$)
- determine a value (how?)
Continue as as long as necessary
Select the next variable
input_order,first_fail,smallest,…dom/wdeg,FBA,CHS,ABS, …
Choose a value
min,max,med, …
Topping
- Combining searches
- Restarting:
geo,luby - Meta-strategy:
lc,cos - Phase saving,
- Best
Define your own
solver.setSearch(Search.intVarSearch(
variables -> Arrays.stream(variables)
.filter(v -> !v.isInstantiated())
.min((v1, v2) -> closest(v2, map) - closest(v1, map))
.orElse(null),
v -> closest(v, map),
DecisionOperator.int_eq,
planes
));
Turnkey enumeration strategies
// Override the default search strategy
solver.setSearch(
Search.lastConflict(
Search.domOverWDegSearch(vars)));
// possibly combined with restarts
solver.setLubyRestart(2, new FailCounter(model, 2), 25000);
solver.findSolution();
Have a look at the Search factory.
Monitoring
Information on research
It is possible to have insights on the search process
solver.showShortStatistics();
while(solver.solve()){};
Or to execute code on solutions using monitors:
solver.plugMonitor((IMonitorSolution) () -> {
// do something here
});
Limits
The search space exploration can be limited.
solver.limitTime("10s");
solver.limitSolution(5);
solver.findAllSolutions();
The first limit reached stops the search.
