Constraints
(and propagators)
A constraint
- represents a problem's requirements or limitations,
- defines a relationships among variables,
- expresses conditions that must be satisfied by the values assigned to the variables,
- is equipped with a filtering algorithm.
For example: $X < Y$
The goal of constraint programming is to find a combination of variable assignments that simultaneously satisfies all the specified constraints.
Basic constraints
| Constraint | Syntax | Comment |
|---|---|---|
| $x + y = z$ | m.arithm(x,"+",y,"=",z) |
Up to 3 variables |
| $\sum_i C_i\cdot X_i = 11$ | m.scalar(X,C,"=",11) |
See also m.sum(x,op,c) |
| $x\times y = z$ | m.times(x,y,z) |
Alt. Euclidean division |
| $y = |x|$ | m.absolute(y,x) |
Or view: y = m.abs(x) |
| $ |x-y | > 3$ | m.distance(x,y,">", 3) |
|
| $z = \max(x,y)$ | m.max(z,x,y) |
Alt. $\min$ |
| $\bigvee_i B_i$ | m.or(B) |
Alt. m.and(B) |
Adding a constraint to the model
Once a constraint has been created, it must be activated or reified
| Action | Syntax |
|---|---|
| Activate $c$ | c.post(); |
| $c \iff b$ | c.reifyWith(b);BoolVar b = c.reify(); |
| $c \implies b$ | c.implies(b); |
| $b \implies c$ | c.impliedBy(b); |
What if you want to express such a a non-linear constraint 🔋 ?

In extension
This can be achieved with a Table constraint
Model m = new Model();
IntVar c = m.intVar("SoC", 0, 100);
IntVar v = m.intVar("cV", 1140, 1280);
Tuples tuples = new Tuples();
tuples.add(100, 1273);
tuples.add(90, 1240);
tuples.add(80, 1235);
//...
tuples.add(20, 1195);
tuples.add(10, 1151);
m.table(c, v, tuples).post();
Types of Table constraints
Allowed tuples
Model m = new Model();
IntVar[] xs = m.intVarArray("x", 3, 1, 3);
// all equal
Tuples tuples = new Tuples();
tuples.add(1, 1, 1);
tuples.add(2, 2, 2);
tuples.add(3, 3, 3);
m.table(xs, tuples).post();
Forbidden tuples
Model m = new Model();
IntVar[] xs = m.intVarArray("x", 3, 1, 3);
// *not* all equal
Tuples tuples = new Tuples(false);
tuples.add(1, 1, 1);
tuples.add(2, 2, 2);
tuples.add(3, 3, 3);
m.table(xs, tuples).post();
Universal value
Like '*' symbol in regular expression.
Model model = new Model();
IntVar[] xs = m.intVarArray("x", 3, 0, 3);
Tuples ts = new Tuples();
int star = 99;
ts.setUniversalValue(star);
ts.add(3, star, 1);
ts.add(1, 2, 3);
ts.add(2, 3, 2);
model.table(xs, ts).post();
Hybrid tuples
Model model = new Model();
IntVar[] xs = m.intVarArray("x", 3, 1, 3);
HybridTuples tuples = new HybridTuples();
tuples.add(ne(1), any(), eq(3));
tuples.add(eq(3), le(2), ne(1));
tuples.add(lt(3), eq(2), ne(b));
tuples.add(gt(2), ge(2), any());
model.table(xs, tuples).post();
It is also possible to express a constraint from a variable
Expressions
| Family | Syntax |
|---|---|
| Arithmetic | x.neg() x.abs() x.sqr()x.add(i, …) x.sub(i, …) x.div(i) x.mod(i) x.pow(i) x.dist(i) x.max(i, …) x.min(i, …) |
| Relational | x.eq(i) x.ne(i) x.in(i, …) x.nin(i, …)x.lt(i) x.le(i) x.gt(i) x.ge(i) |
| Logical | x.not() x.imp(r) x.iff(r) x.ift(r1, r2) x.and(r, …) x.or(r, …) x.xor(r, …) |
$i$ is either an
int, a IntVar or an arithmetical expression,
$r$ is a relational expression.
Example
$(x = y + 1) \lor (x+2 \leq 6)$
IntVar x = //...
IntVar y = //...
x.eq(y.add(1)).or(x.add(2).le(6)).post();
Adding an expression to the model
Here again, there are different ways to work with an expression $e$, depending on its type:| Syntax | Ar. | Re. | Lo. |
|---|---|---|---|
e.post(); |
❌ | ✅ | ✅ |
c = e.decompose(); c = e.extension(); |
❌ ❌ |
✅ ✅ |
✅ ✅ |
x = e.intVar();b = e.boolVar(); |
✅ ❌ |
❌ ✅ |
❌ ✅ |
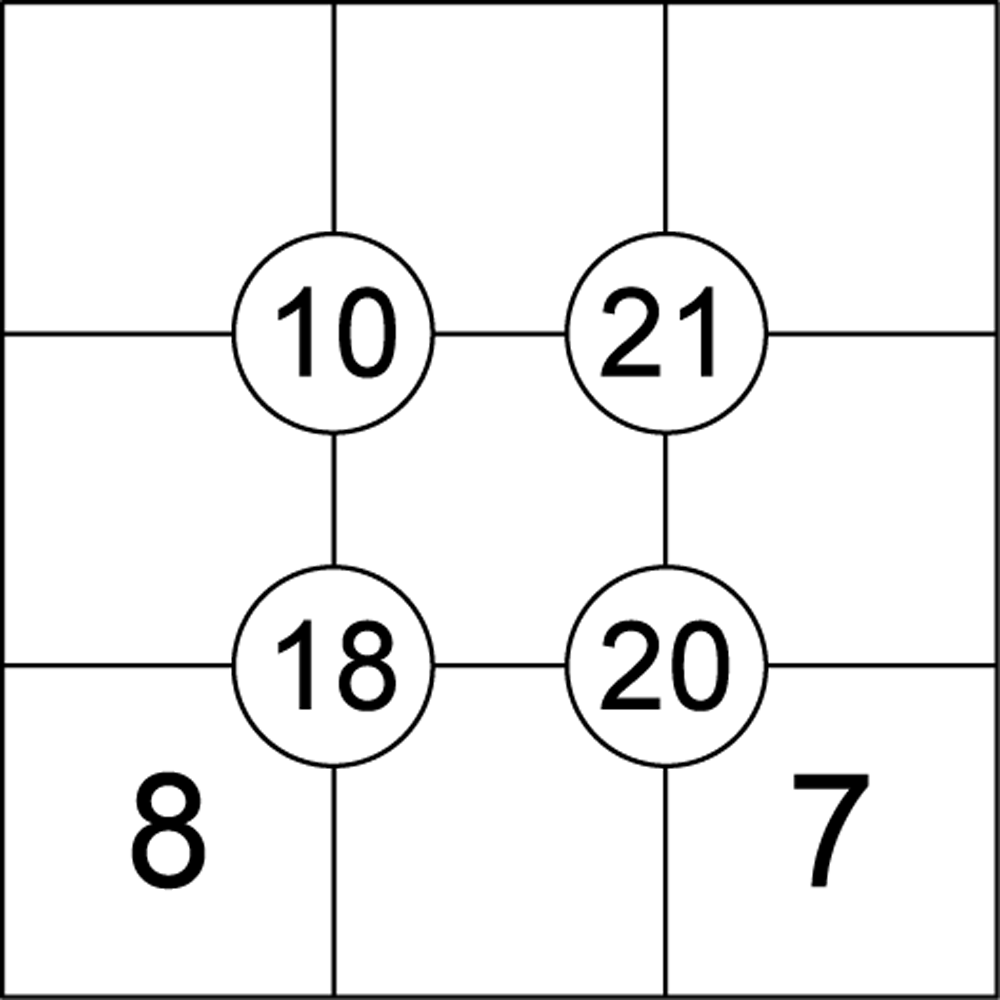
Sujiko
The puzzle takes place on a 3x3 grid with four circled number clues at the centre of each quadrant which indicate the sum of the four numbers in that quadrant.
The numbers 1-9 must be placed in the grid, in accordance with the circled clues, to complete the puzzle.
Empty grid
A Model
- Parameters
- $S_0, S_1, S_2, S_3$: the four circled number clues
- $f_{i,j}$: some fixed cells
- Variables
- $\forall i,j \in [\![0,2]\!]^2, x_{i,j} \in [\![1,9]\!]$
- Constraints
- $\forall i, i’, j, j’ \in [\![0,2]\!]^4, (i,j)\neq(i’,j’), x_{i,j} \neq x_{i’,j’}$
- $\forall i \in [\![0,3]\!], k = \frac{i}{2}, \ell = i \mod 2,$ $x_{k,\ell} + x_{k + 1,\ell} + x_{k,\ell + 1} + x_{k + 1,\ell +1} = S_i$
- +clues
Hints
model.allDifferent(IntVar[])
model.sum(IntVar[], String, int)
model.arithm(IntVar, String, int)
int[] circles = new int[]{10, 21, 18, 20};
int[] clues = new int[]{0, 0, 0, 0, 0, 0, 8, 0, 7};
private IntVar[] quadrant(IntVar[][] grid, int i) {
int x = i / 2;
int y = i % 2;
return new IntVar[]{grid[x][y], grid[x + 1][y], grid[x][y + 1], grid[x + 1][y + 1]};
}
A Choco-solver code
Model model = new Model("Sujiko");
IntVar[][] grid = model.intVarMatrix("x", 3, 3, 1, 9);
// Constraint: "The numbers 1-9 must be placed in the grid"
// implies that all values must be different
model.allDifferent(ArrayUtils.flatten(grid)).post();
// Constraint: "each quadrant which indicate the sum of the four numbers in that quadrant"
for (int i = 0; i < 4; i++) {
IntVar[] cells = quadrant(grid, i);
model.sum(cells, "=", circles[i]).post();
}
// Constraint: "the clues"
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
if (clues[i * 3 + j] != 0) {
model.arithm(grid[i][j], "=", clues[i * 3 + j]).post();
}
}
}
while (model.getSolver().solve()) {
System.out.println("Solution:");
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
System.out.print(grid[i][j].getValue() + " ");
}
System.out.println();
}
}
if (model.getSolver().getSolutionCount() == 0) {
System.out.println("No solution found");
}
Output
Solution:
1 4 9
3 2 6
8 5 7