Analogy with Sudoku

We reached the Sudoku point

When trying to explain how constraint programming works, it is common to draw a parallel with sudoku.

At modelling step

  • One must write a value in $[1,9]$ in each cell

    • ➡️ a variable and a domain

  • Such that each digit is used exactly once per row , per column and per square

    • ➡️ sets of $\neq$ constraints

At solving step

Local reasonning

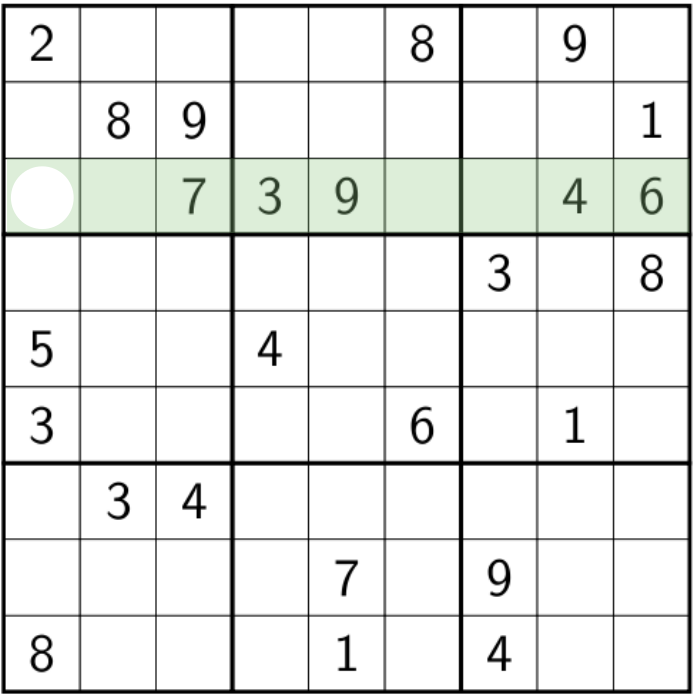
This is an alt
Each constraint infers on a local view.

Filtering

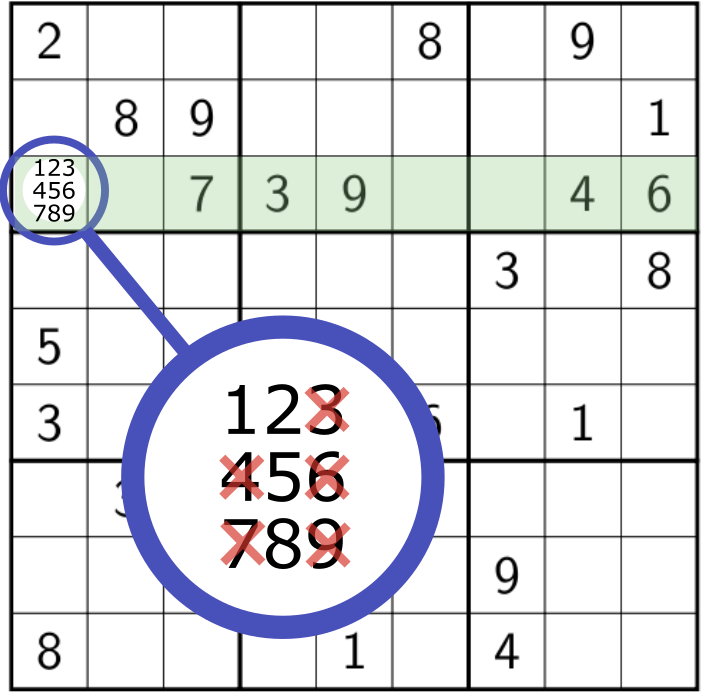
This is an alt
Impossible values are removed
from a variable's domain

Propagation

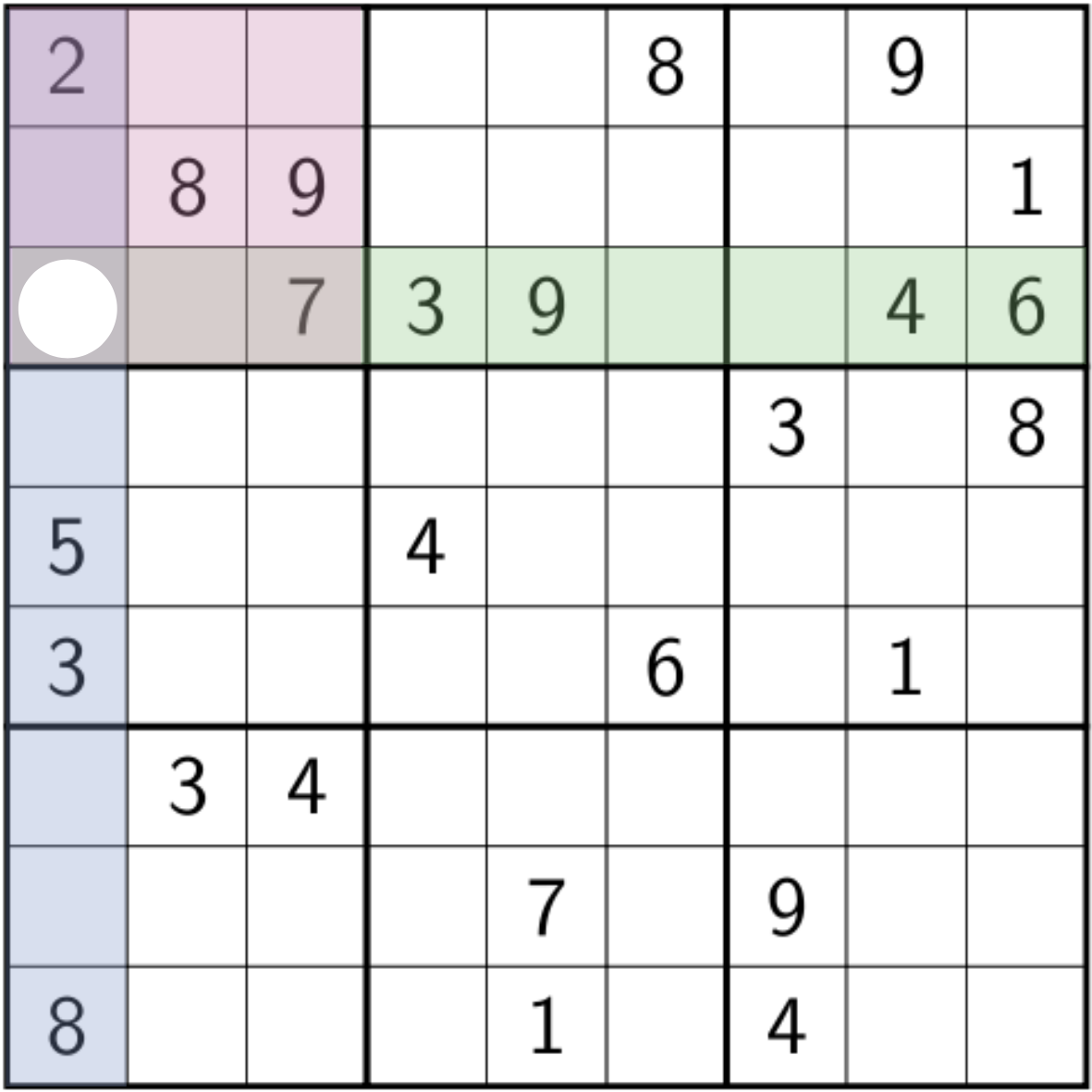
This is an alt
The information is shared between the constraints through the variables

On devil sudoku, one has to make assumptions.

And validate them by propagation.

A 4x4 sudoku example

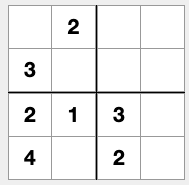
This is an alt 
import model as m

n = 4
variables = {}
for i in range(1, n + 1):
    for j in range(1, n + 1):
        variables["x" + str(i) + str(j)] = {k for k in range(1, n + 1)}
# fix values
variables["x12"] = [2]
variables["x21"] = [3]
variables["x31"] = [2]
variables["x32"] = [1]
variables["x33"] = [3]
variables["x41"] = [4]
variables["x43"] = [2]

zones = []
# rows
zones.append(["x11", "x12", "x13", "x14"])
zones.append(["x21", "x22", "x23", "x24"])
zones.append(["x31", "x32", "x33", "x34"])
zones.append(["x41", "x42", "x43", "x44"])
# columns
zones.append(["x11", "x21", "x31", "x41"])
zones.append(["x12", "x22", "x32", "x42"])
zones.append(["x13", "x23", "x33", "x43"])
zones.append(["x14", "x24", "x34", "x44"])
# square
zones.append(["x11", "x12", "x21", "x22"])
zones.append(["x13", "x14", "x23", "x24"])
zones.append(["x31", "x32", "x41", "x42"])
zones.append(["x33", "x34", "x43", "x44"])

cs = []
for z in zones:
    for j in range(0, n):
        for k in range(j + 1, n):
            cs.append(NotEqual(z[j], z[k]))

sols = []
m.dfs(variables, cs, sols, nos=0)
print(len(sols), "solution(s) found")
u_sol = sols[0]
for i in range(4):
		print(u_sol[i * 4:i * 4 + 4])

1 solution

1 solution(s) found
[1, 2, 4, 3]
[3, 4, 1, 2]
[2, 1, 3, 4]
[4, 3, 2, 1]